En este capítulo y en el próximo seguiremos el desarrollo de una cantidad de notables paradojas geométricas; algunas son conocidas y otras se publican aquí por primera vez. Todas ellas involucran el corte y readaptación de las partes de una figura. Una vez hecha la readaptación, una porción de la figura original (ya sea una parte de su superficie, o una de las series de dibujos que se que se han hecho sobre la figura) aparentemente se ha esfumado sin dejar rastro. Cuando se vuelven a plantear las piezas en su forma original, el área o dibujo desaparecidos reaparecen misteriosamente. Por estas curiosas desapariciones y reapariciones, las presentes paradojas se consideran dentro de la magia matemática.
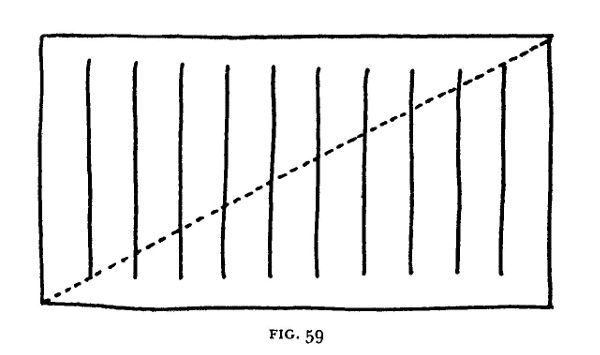
Nadie, que yo sepa, ha reconocido el hecho de que las diversas paradojas que discutiremos aquí operan todas por un principio común. A falta de un nombre mejor, lo llamaremos Principio de Distribución Oculta. La siguiente paradoja elemental (Fig. 59), que es muy antigua, pondrá el principio en claro.
El lector notará que en el rectángulo se han colocado diez líneas verticales de igual longitud, de tal manera que si se sigue la diagonal punteada de izquierda a derecha, se observa una progresiva disminución en el largo de los segmentos que están por encima de la diagonal y un aumento equivalente en el largo de los segmentos que están por debajo. Ahora cortamos el rectángulo a lo largo de la diagonal, y vamos a deslizar la parte inferior hacia abajo y a la izquierda hasta la posición que muestra la Figura 60.

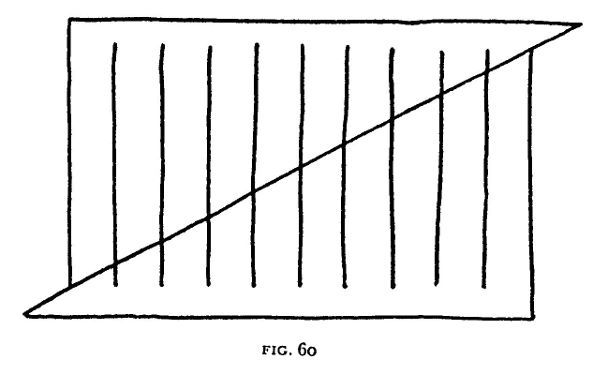
Si usted cuenta las líneas verticales de esta última figura, descubrirá que ahora son sólo nueve. ¿Qué línea se esfumó, y a dónde fue? Deslice la parte inferior de vuelta a su posición anterior y la línea desvanecida reaparece. Pero ¿cuál es la línea que regresó, y de dónde vino?
En una primera aproximación éstas son preguntas desconcertantes; pero con sólo un análisis superficial uno se da cuenta de que no es una línea individual la que se esfuma. Lo que sucede es que ocho de las diez líneas se han quebrado en dos segmentos; esos dieciséis segmentos se redistribuyen luego para formar nueve líneas, algo más largas que las anteriores. Como el aumento en la longitud de cada línea es pequeño, no se nota en forma inmediata. En realidad, la suma de todos estos ligeros aumentos es exactamente igual al largo de una de las líneas originales.
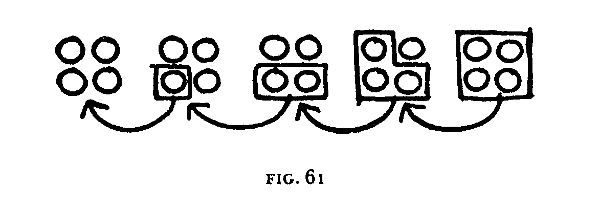
El mecanismo de la paradoja tal vez pueda aclararse aún más si consideramos cinco grupos de bolitas que contengan cuatro bolitas cada uno. Desplacemos una bolita del segundo grupo al primero, dos bolitas del tercer grupo al segundo, tres bolitas del cuarto grupo al tercero, y finalmente movamos las cuatro bolitas del quinto grupo al cuarto; La Figura 61 pondrá esto en claro.
Después de haber hecho estos desplazamientos, veremos que sólo quedan cuatro grupos de bolitas. Obviamente es imposible responder a la pregunta «¿Qué grupo desapareció?» porque tres de los grupos se quebraron y redistribuyeron de tal manera que cada grupo ganó una bolita adicional. Por supuesto, esto es exactamente lo que ocurre en la paradoja de las líneas. Como el desplazamiento se hace a lo largo de la diagonal, al reacomodarse los segmentos de las líneas quebradas cada línea aumenta ligeramente su longitud.
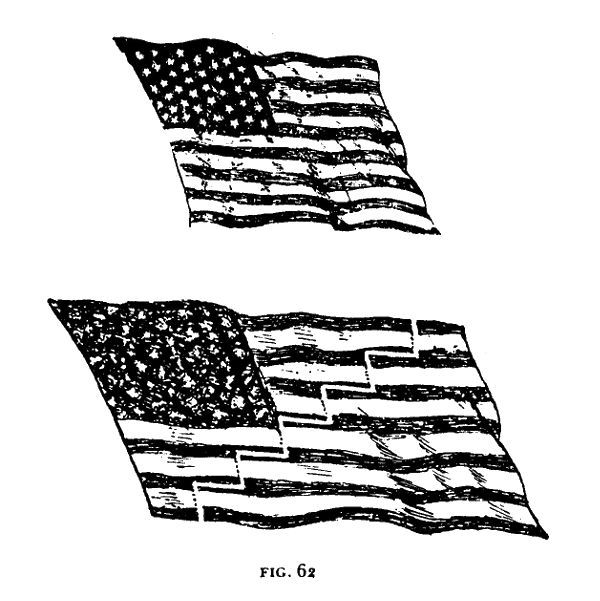
Sam Loyd propuso un interesante enigma de cortes basado sobre esta paradoja. El problema consiste en cortar una bandera de los Estados Unidos de quince franjas en el menor número de piezas que puedan reacomodarse para formar una bandera de trece franjas. La Figura 62, tomada de la CYCLOPEDIA OF 5000 PUZZLES de Loyd, muestra cómo se resuelve el problema cortando la bandera en dos piezas.[8]
Consideramos ahora otras maneras en que se puede elaborar la paradoja de las líneas para que las desapariciones y reapariciones resulten más interesantes. Obviamente, las líneas pueden ser sustituidas por figuras bidimensionales. Podemos usar figuras de lápices, cigarros, ladrillos, sombreros altos, vasos de agua, y otros objetos que puedan dibujarse con lados verticales, de tal manera que la figura pueda acomodarse antes y después del desplazamiento. Con un poco de ingenio artístico, se pueden utilizar figuras más complicadas. Considere, por ejemplo, la cara que desaparece en la Figura 63.
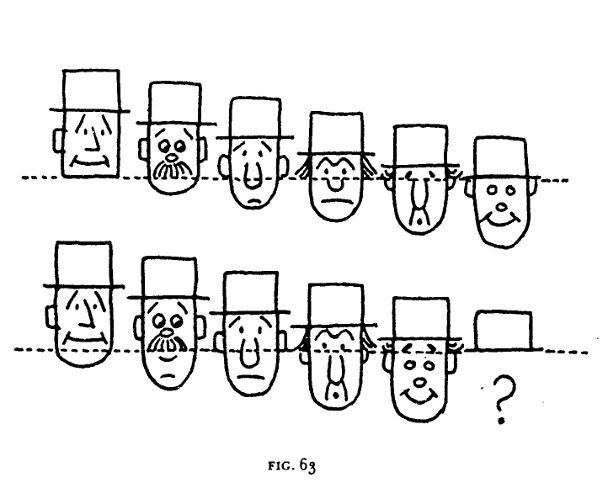
Cuando la banda inferior se desplaza hacia la izquierda de la manera indicada, permanecen todos los sombreros ¡pero una de las caras se esfuma por completo! Es inútil preguntar cuál de las caras desaparece, porque una vez hecho el desplazamiento cuatro caras se han quebrado en dos partes, y las partes se redistribuyeron de tal modo que cada cara aumenta un poco: aquí una nariz más larga, allá un poco más de mentón, etcétera. Pero la distribución se disimula ingeniosamente, y la desaparición de una cara entera es por supuesto, mucho más impactante que el desvanecimiento de una línea.
Sam Loyd habrá pensado en estas líneas cuando inventó y patentó su famoso enigma «¡Fuera de Este Mundo!», en 1896. Fue su más grande creación. En vida de Loyd se vendieron declaradamente más de diez millones de ejemplares en los Estados Unidos y en el extranjero. Durante 1897 fue distribuido por el Partido Republicano para promover la campaña presidencial de McKinley. En el «Inauditorio» de Robert Ripley, en la Exposición Siglo del Progreso que tuvo lugar en Chicago en 1933, el «relator» que estaba fuera del edificio usó una enorme reproducción en madera del juego para atraer multitudes. Contaba con un puntero los trece guerreros chinos, hacía girar rápidamente la rueda, la detenía en la posición deseada, y entonces contaba las figuras de nuevo para demostrar que uno de los guerreros se había esfumado. El juego original de Loyd, tal como él mismo lo dibujó, aparece reproducido en la Figura 64. (Para el relato que hace Loyd del invento de esta paradoja, ver «The Prince of Puzzle-makers», revista Strand, Vol. 34, 1907, p. 771).
Lo que hizo Sam Loyd fue simplemente curvar la paradoja de las líneas en una forma circular y sustituir las líneas por guerreros chinos. En la ilustración que se presenta hay doce figuras. Si se corta el círculo, y luego se lo hace rotar en el sentido de las agujas del reloj hasta que la flecha señale el N. E., las partes quebradas de las figuras se reacomodan entre sí para formar trece guerreros. Cuando se hace volver la flecha al N. O., la figura extra se desvanece.
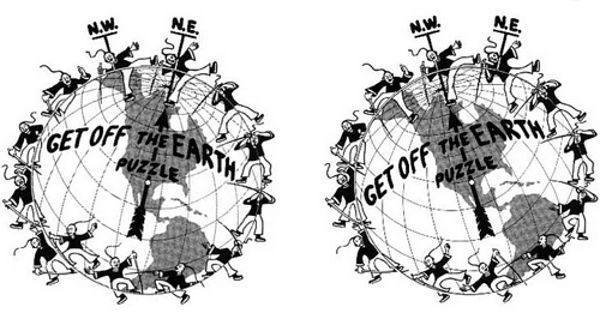
Usted notará que cuando se ven trece guerreros, dos de ellos se oponen directamente el uno al otro en la parte inferior izquierda del círculo. Estas dos figuras corresponden a las líneas de los extremos de la paradoja de las líneas. Es necesario que cada uno de ellos pierda una pequeña porción de pierna, y al ponerlos juntos cuando se gira la rueda, la pérdida resulta menos evidente. Se puede hacer girar más la rueda para producir catorce guerreros, quince, o más, pero a medida que el número aumenta, resulta más obvio que cada figura se reduce para proveer sustancia a las figuras nuevas.
Los guerreros están dibujados con un ingenio mucho mayor de lo que se podría pensar en una primera inspección. Por ejemplo, para que las figuras puedan mantenerse en posición erecta en tomo del globo, en algún punto es necesario que una pierna izquierda se convierta en una pierna derecha, y en otro punto que una pierna derecha se convierta en una izquierda.
Durante 1896, después de que el juego hizo su aparición, Loyd publicó (en su columna dominical de acertijos del Daily Eagle de Brooklyn) más de cincuenta cartas de lectores que ofrecían diversas explicaciones, muchas de ellas hilarantes. Algunos lectores se sintieron impulsados a la versificación. «Yo solía ser un hombre feliz…» comienza un poema de Wallace Vincent, que continúa así:
Pero ahora me encuentro solitario
Con un aspecto que da tristeza.
Hundido el ojo, el cuerpo magro,
Y ardo en lunática fiereza.
La única ventana de mi habitación
Está cruzada por barras de acero.
Los asistentes empujan mi colación
A través de la puerta, por un agujero.
Me arrastro de la noche a la mañana
En una sola esquina de mi habitación.
Hay algo en mi mano que contemplo
Con melancolía y expectación.
Lo empujo hacia arriba, lo empujo hacia abajo,
Los cuento a todos una vez más.
Doy entonces un grito azorado
y azoto el piso hasta reventar.
Ahorro al lector las estrofas finales de esta triste balada. Sam Loyd diseñó en 1909 un enigma similar llamado «Teddy y los Leones», que representaba a Theodore Roosevelt, siete leones y siete nativos africanos. Los nativos y los leones se alternaban en tomo del círculo, un grupo en espiral hacia adentro y el otro grupo en espiral hacia afuera. Por consiguiente, al girar la rueda se producían ocho leones y seis nativos. El juego es ahora una rara pieza de colección. El único ejemplar que he visto, perteneciente al Dr. Vosburgh Lyons, fue distribuido como anuncio del Museo Edén, un museo de cera de Manhattan. Parte del texto al dorso de la tarjeta dice:
«Este misterio fue diseñado por Sam Loyd, el hombre que inventó Cerdos a Cuerpo de Rey, el Enigma de los Quince Bloques, el Parchís, etcétera, pero ésta es su obra mayor. Usted verá un hombre NEGRO convertirse en un león AMARILLO delante de sus mismos ojos, pero cuanto más lo investigue menos lo comprenderá. Dice el Profesor Rogers. “Es una ilusión óptica, o está impreso con tinta fosfórico-fluorescente, no sé”. Envíe la mejor respuesta que se le ocurra para explicar la misteriosa desaparición del hombre negro, al Editor de Acertijos de The Globe, ya que todas las semanas se regalarán veinticinco entradas gratis al Museo Edén a las mejores respuestas…».
Theodore L. DeLand, Jr., un grabador y mago aficionado de Filadelfia, patentó en 1907 otra ingeniosa variante de la paradoja de las líneas verticales. La publicó en diversas formas, una de las cuales se muestra en la Figura 65.
Se corta la tarjeta por la línea horizontal AB y por la línea vertical CD, con lo que se forman tres piezas. Al intercalar las posiciones de los dos rectángulos inferiores se obtiene el mismo resultado que al deslizar la parte inferior en la paradoja de las líneas. Uno de los naipes desaparece. Una ventaja de esta construcción es que la secuencia progresiva y escalonada de las figuras se quiebra en secciones, de manera que las figuras parecen estar desparramadas sobre la tarjeta de un modo más azaroso. Para oscurecer aún más el arreglo, DeLand agregó algunos otros naipes que no juegan parte alguna en la paradoja.

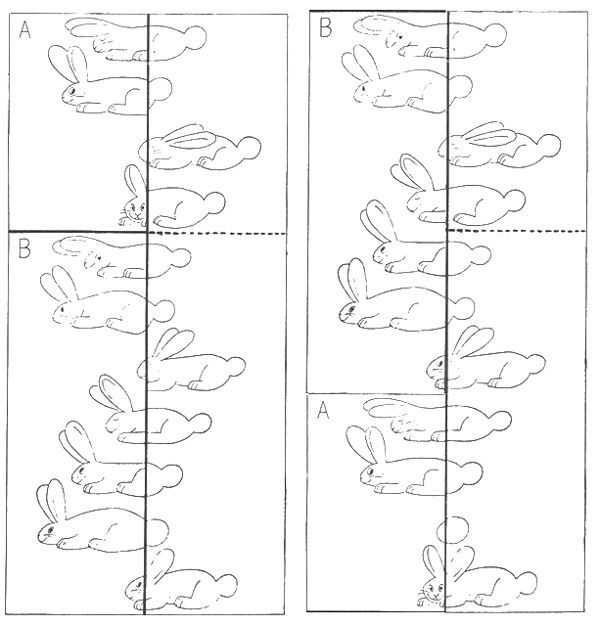
La paradoja de DeLand puede obviamente ser elaborada con figuras más complicadas: caras, figuras humanas, animales, etcétera. La Figura 66 reproduce una variante diseñada por mí para la sección de Entretenimiento Familiar de Parents Magazine, abril de 1952. Como se ve, simplemente giré la construcción de DeLand a una posición vertical y reemplacé naipes por conejos. Cuando se intercambian los rectángulos Ay B, un conejo desaparece y en su lugar aparece un huevo de Pascua. Hubiera sido posible hacer que el conejo se esfumara por completo dejando un espacio vacío, pero se agrega un ameno toque pascual porque la punta de una nariz y el extremo de una cola se combinan perfectamente para formar el huevo que dejó el conejo antes de partir.
Si en lugar de desplazar A y B, la mitad derecha se corta por la línea de puntos y se intercambian las dos piezas, el número de conejos aumentará a doce. Sin embargo, un conejo pierde sus orejas y se producen otros resultados grotescos.
Faltaba que Mel Stover, de Winnipeg, Canada, agregara el toque final a la idea de DeLand. En 1951 Stover diseñó una tarjeta con dos conjuntos de figuras entrelazadas (Fig. 67) a la manera del enigma de Sam Loyd «Teddy y los Leones». Uno de los conjuntos está formado por vasos de cerveza, y el otro por caras de hombre. Cuando se hace el desplazamiento desaparece una cara y en cambio aparece un vaso de cerveza adicional; presumiblemente, un hombre se ha convertido en vaso de cerveza. El uso de conjuntos entrelazados de figuras abre muchas posibilidades mágicas. Stover, por ejemplo, diseñó otra tarjeta que representa una cantidad de lápices, algunos rojos y otros azules (Fig. 68). Al desplazar dos partes de la figura, un lápiz azul se desvanece y aparece un lápiz rojo.

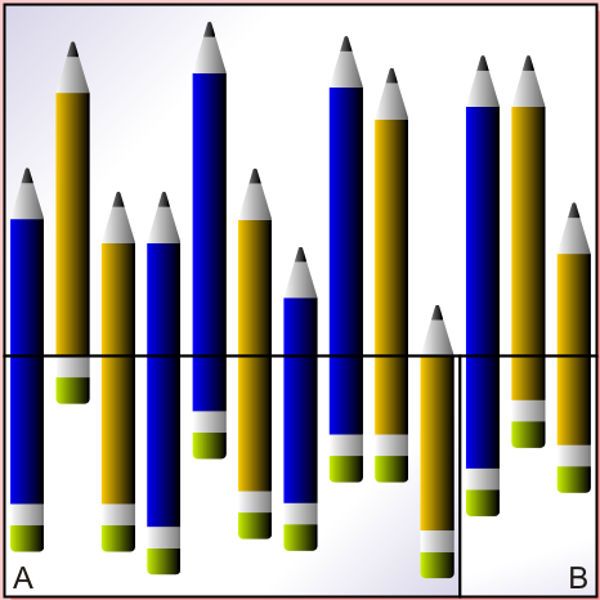
Tal como señala el señor Stover, esta paradoja puede construirse en forma tridimensional, con el uso de lápices verdaderos montados sobre paneles de madera. En realidad, todas las paradojas que se discuten en este capítulo y en el próximo pueden diseñarse en forma tridimensional, aunque en la mayor parte de los casos esta nueva dimensión no agrega nada.
La paradoja de DeLand, en todas sus formas, debe cuidar que el número de unidades en las dos piezas a desplazar sean primos entre sí, es decir, no deben tener otro denominador común más que 1. En la paradoja del conejo, por ejemplo, la parte A contiene 4 unidades y la parte B contiene 7. Si el número total de unidades es primo, como 11 en este caso, entonces la línea divisoria entre A y B puede hacerse en cualquier parte, porque en una cantidad prima ningún par de números puede tener un denominador común. En todas las formas de la paradoja, las figuras pueden manejarse como para que la desaparición se produzca en el lugar de la fila que se desee.
El principio de DeLand se aplica fácilmente a la forma circular de Sam Loyd. En lugar de que los guerreros chinos avancen gradualmente en espiral hacia adentro, las figuras pueden quebrarse en grupos más pequeños y escalonados como en la forma de DeLand. En este caso, el círculo debe girar la distancia de varias unidades en lugar de una. La única ventaja consiste en que las figuras parecen estas puestas al azar, y en consecuencia el principio de la paradoja queda mejor camuflado.
El círculo puede plantearse en forma tridimensional, por supuesto, colocando simplemente las figuras en tomo del exterior de un cilindro, cono o esfera, cortados como para que se pueda rotar una mitad con respecto a la otra.