Acertijos topológicos
Uno de los teoremas fundamentales de la topología es el teorema de la curva de Jordán (Así llamado por el matemático francés Camille Jordán). Este teorema postula que cualquier curva simple cerrada (una curva unida en los extremos y que no se cruza a sí misma), divide la superficie del plano en dos regiones, un adentro y un afuera (figura 1). El teorema parece bastante obvio, pero en realidad es de difícil demostración.

Si trazamos una curva simple cerrada muy sinuosa, como la que muestra la figura 2, no es fácil decir de inmediato si cierto punto, como el señalado por medio de la crucecita, está dentro o fuera. Por supuesto que podemos descubrirlo sí seguimos con un lápiz el trayecto desde este punto hasta el borde de la curva para ver si conduce o no afuera.

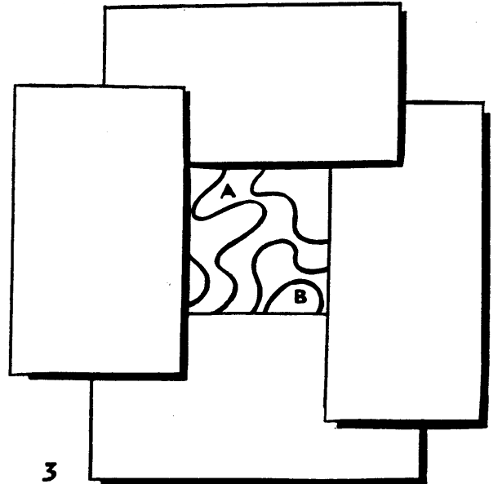
La figura 3 muestra sólo una pequeña porción interior de una curva simple cerrada. El resto de la curva, por los cuatro lados, está oculta a la vista por hojas de papel, de modo que no hay manera de seguir con el lápiz el trayecto que va desde las regiones visibles hasta el borde de la curva, para ver si conduce o no afuera. Se nos dice que la región marcada como A está adentro de la curva.
¿La región B está adentro o afuera, y cómo lo sabes?