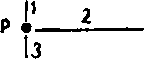
Acertijos topológicos

SOLUCIÓN

Es imposible dibujar los cinco ladrillos con tres trazos; hay una manera simple de probarlo.

Cuando tres segmentos de línea se reúnen en un punto, como lo muestra la figura 4, es obvio que ese punto debe señalar el final al menos de un trazo. También podría ser el final de tres trazos, pero eso no nos interesa. Sólo nos importa el hecho de que al menos una línea debe terminar en el punto P de la ilustración.

Cuenta el número de puntos de la figura 1, que muestra los ladrillos, donde se unen tres segmentos de líneas. Hay ocho puntos de ésos. Cada uno de ellos debe señalar el final de al menos un trazo, de modo que la figura completa contiene como mínimo ocho finales de trazos. Ningún trazo puede tener más de dos extremos, por lo que la figura no puede dibujarse con menos de cuatro trazos.

Éste es un ejemplo simple de lo que los matemáticos llaman una prueba de imposibilidad. Con mucha frecuencia, en la historia de las matemáticas, se desperdicia una gran cantidad de tiempo intentando resolver un problema, como el de trisecar un ángulo con sólo un compás y una regla, que no tiene solución. Por eso es muy importante investigar las pruebas de imposibilidad. Otro excelente ejemplo de ese tipo de prueba se encontrará en el acertijo de los cinco tetrominós de la sección siguiente.