El cálculo proposicional constituye un ejemplo de un sistema matemático en el que se alcanzan plenamente los objetivos de la teoría de la demostración de Hilbert. Ciertamente, este cálculo codifica solamente un fragmento de la lógica formal, y su vocabulario y su aparato formal no son suficientes para desarrollar ni siquiera la aritmética elemental, pero el programa de Hilbert no es tan limitado. Puede ser aplicado con éxito a sistemas más amplios, cuyo carácter, a la vez consistente y completo, puede ser demostrado mediante un razonamiento metamatemático. Una prueba absoluta de consistencia, por ejemplo, se ha logrado para un sistema de aritmética que permita la adición de números cardinales, aunque no la multiplicación. Pero ¿es el método finitista de Hilbert lo suficientemente potente como para demostrar la consistencia de un sistema como Principia, cuyo vocabulario y cuyo aparato lógico son adecuados para expresar toda la aritmética y no simplemente un fragmento de ella? Los repetidos intentos de construir una prueba de este tipo resultaron infructuosos; y la publicación en 1931 del trabajo de Gödel demostró finalmente que no podían por menos de fracasar todos los esfuerzos que se desenvolvieran dentro de los estrictos límites del primitivo programa de Hilbert.

¿Qué es lo que estableció Gödel y cómo demostró sus resultados? Sus principales conclusiones son dos. En primer lugar (aunque no sea este el puesto que ocupa en el razonamiento de Gödel) demostró que es imposible presentar una prueba metamatemática de la consistencia de un sistema lo bastante comprensivo como para contener toda la aritmética, a menos que se empleen en la prueba reglas de deducción que difieran en ciertos aspectos esenciales de las reglas de transformación utilizadas para derivar teoremas dentro del sistema. Indudablemente, una prueba así posee gran valor e importancia. Sin embargo, si el razonamiento se basa en reglas de deducción mucho más potentes que las reglas del cálculo aritmético, de tal modo que la consistencia de las hipótesis contenidas en el razonamiento esté tan sujeta a la duda como lo está la consistencia de la aritmética, la prueba no produciría sino un especioso triunfo; sería matar un dragón solamente para crear otro. En cualquier caso, si la prueba no es finitista, no cubre los objetivos del programa original de Hilbert; y la argumentación de Gödel hace que sea improbable el que pueda darse una prueba finitista de la consistencia de la aritmética.

La segunda importante conclusión de Gödel es aún más sorprendente y revolucionaria, porque demuestra la existencia de una fundamental limitación en la potencia del método axiomático. Gödel demostró que los Principia, o cualquier otro sistema dentro del cual pueda desarrollarse la aritmética, es esencialmente incompleto. En otras palabras: dado cualquier conjunto consistente de axiomas aritméticos, existen proposiciones aritméticas verdaderas que no pueden ser derivadas de dicho conjunto. Este decisivo punto merece ser ilustrado con un ejemplo. Las matemáticas abundan en proposiciones generales a las que no se ha encontrado ninguna excepción que hasta ahora haya frustrado todo intento de prueba. Un ejemplo clásico es el conocido como «teorema de Goldbach», el cual afirma que todo número par es la suma de dos números primos. Jamás se ha encontrado ningún número par que no sea la suma dos números primos; sin embargo, nadie ha logrado encontrar una prueba de que la conjetura de Goldbach se aplique sin excepción a todos los números pares. Tenemos, pues, aquí un ejemplo de una proposición aritmética que puede ser verdadera, pero que puede no ser derivable de los axiomas de la aritmética. Supongamos ahora que la conjetura de Goldbach fuese, en efecto, universalmente verdadera, aunque no derivable de los axiomas. ¿Qué decir ante la sugerencia de que, en este caso, los axiomas podrían ser modificados o aumentados hasta hacer que las proposiciones hasta el momento indemostrables (tal como la de Goldbach en nuestra hipótesis) fuesen derivables en el sistema ampliado? Los resultados obtenidos por Gödel demuestran que, aunque la hipótesis fuese correcta, la sugerencia no suministraría remedio definitivo a la dificultad. Es decir, que aun cuando los axiomas de la aritmética sean ampliados con un número indefinido de otros axiomas verdaderos, siempre quedaran verdades aritméticas que no son formalmente derivables del conjunto ampliado^[15].

¿Cómo demostró Gödel estas conclusiones? Hasta cierto punto, la estructura de su argumentación está moldeada, como el mismo hizo notar, sobre el razonamiento implicado en una de las antinomias lógicas conocida como la «paradoja richardiana», propuesta por el matemático francés Jules Richard en 1905. Explicaremos en que consiste esta paradoja.

Considérese un lenguaje (por ejemplo, el español) en el que se puedan formular y definir las propiedades puramente aritméticas de los números cardinales. Examinemos las definiciones que pueden ser expresadas en dicho lenguaje. Resulta claro que, so pena de caer en círculo vicioso o regreso al infinito, no pueden definirse explícitamente algunos términos que hacen referencia a propiedades aritméticas —ya que no podemos definirlo todo y debemos empezar en alguna parte—, aunque, presumiblemente, pueden ser comprendidos de alguna otra manera. Para el objeto que nos ocupa, es indiferente cuáles sean los términos no definidos o «primitivos»; podemos, por ejemplo, dar por supuesto que comprendemos lo que se quiere decir con «un número entero es divisible por otro», etc. La propiedad de ser un número primo puede ser definida como «no divisible por ningún otro número entero más que por sí mismo y la unidad»; la propiedad de ser un cuadrado perfecto puede ser definida como «ser el producto de algún número entero por sí mismo», etc.

Fácilmente podemos ver que cada una de tales definiciones contendrá solamente un número finito de palabras y, por consiguiente, solo un número finito de letras del alfabeto. Siendo esto así, las definiciones pueden ser ordenadas en una serie: una definición precederá a otra si el número de letras de la primera es menor que el número de letras de la segunda; y si dos definiciones tienen el mismo número de letras, una de ellas precederá a la otra atendiendo al orden alfabético de las letras contenidas en cada una. Sobre la base de este orden, a cada definición corresponderá un único número entero, que representará el lugar que ocupa la definición en la serie. De este modo, la definición que menos letras tenga corresponderá al número 1, la siguiente definición de la serie corresponderá al 2, y así sucesivamente.

Dado que cada definición está asociada a un único número entero, puede ocurrir en algunos casos que un número entero posea la misma propiedad expresada por la definición con la cual está asociado^[16]. Supongamos, por ejemplo, que la expresión definidora «no divisible por ningún número entero más que por sí mismo y por la unidad» se halla en correlación con el número de orden 17; evidentemente, el 17 tiene la propiedad designada por esa expresión. Por otra parte, supongamos que la expresión definidora «ser el producto de algún número entero por sí mismo» se halla en correlación con el número de orden 15; esta claro que 15 no posee la propiedad designada por la expresión. Describiremos la situación existente en el segundo ejemplo diciendo que el número 15 tiene la propiedad de ser richardiano, y la del primer ejemplo, diciendo que el número 17 no tiene la propiedad de ser richardiano. Hablando en términos más generales, definimos «x es richardiano» como una forma abreviada de declarar «x no tiene la propiedad designada por la expresión definidora con la que se halla relacionado en la serie ordenada de definiciones».

Llegamos ahora a un punto curioso, pero característico, de la proposición en que consiste la paradoja richardiana. La expresión definidora de la propiedad de ser richardiano describe ostensiblemente una propiedad numérica de los enteros. La expresión misma pertenece, por tanto, a la serie de definiciones ya enunciadas antes. De aquí se desprende que la expresión está relacionada con un número entero determinador de su posición. Supongamos que este número es n. Y ahora planteamos la cuestión, con ciertas reminiscencias de la antinomia de Russell: ¿Es n richardiano? El lector puede, sin duda alguna, anticipar la fatal contradicción que amenaza ahora. Porque n es richardiano si, y solamente si, n carece de la propiedad designada por la expresión (definidora) con la que está relacionado (esto es, si carece de la propiedad de ser richardiano). En resumen, n es richardiano si, y solamente si, n no es richardiano; de modo que la declaración «n es richardiano» es verdadera y falsa a la vez.

Debemos hacer notar ahora que la contradicción es, en cierto sentido, una consecuencia derivada de no jugar del todo limpio. Se ha deslizado, por ser útil, una esencial pero tácita hipótesis subyacente bajo la ordenación sucesiva de las definiciones. Se había acordado considerar las definiciones de las propiedades estrictamente aritméticas de los números enteros, es decir, propiedades que pueden formularse con ayuda de nociones tales como las de adición aritmética, multiplicación, etc. Pero entonces, sin previo aviso, se nos invita a que metamos dentro de la serie una definición que se refiere a la notación utilizada para formular las propiedades aritméticas. Más concretamente, la definición de la propiedad de ser richardiano no pertenece a la serie inicialmente proyectada, porque esta definición implica nociones metamatemáticas tales como el número de letras (o signos) que se dan en las expresiones. Podemos soslayar la paradoja de Richard distinguiendo cuidadosamente entre las proposiciones que se producen dentro de la aritmética (que no hacen ninguna referencia a sistema alguno de notación) y las proposiciones acerca de algún sistema de notación en el que se codifica la aritmética.

Existe una evidente falacia en el razonamiento empleado para la construcción de la paradoja de Richard. La construcción sugiere, no obstante, la idea de que cabe la posibilidad de «representar» o «reflejar» declaraciones metamatemáticas acerca de un sistema formal suficientemente amplio dentro del sistema mismo. La idea de la «representación» es sobradamente conocida y desempeña un papel fundamental en muchas ramas de las matemáticas. Se utiliza para la construcción de los mapas ordinarios, en la que las formas existentes en la superficie de una esfera se proyectan sobre un plano, de tal modo que las relaciones entre las figuras del plano reflejan las relaciones entre las figuras de la superficie esférica. Se utiliza en la geometría de coordenadas, que traduce la geometría al álgebra de modo que las relaciones geométricas quedan representadas por otras algebraicas. (El lector recordara la exposición realizada en el capítulo segundo, en el que se explicaba cómo empleó Hilbert el álgebra para demostrar la consistencia de sus axiomas aplicados a la geometría. Lo que en realidad hizo Hilbert fue representar la geometría en el álgebra.) La representación desempeña también un importante papel en la física matemática, donde, por ejemplo, las relaciones entre las propiedades de las corrientes eléctricas se plasman en el lenguaje de la hidrodinámica. Y existe también representación cuando se construye una maqueta antes de abordar la realización de la máquina a su tamaño natural, cuando se somete a observación una pequeña superficie del ala de un avión en un túnel de viento con objeto de apreciar sus propiedades aerodinámicas, o cuando se utiliza un equipo de laboratorio hecho de circuitos eléctricos para estudiar las relaciones entre masas de gran tamaño en movimiento. Presentamos un sugestivo ejemplo visual en la figura 3, que ilustra una especie de proyección, que se efectúa en una rama de las matemáticas conocida como geometría proyectiva.

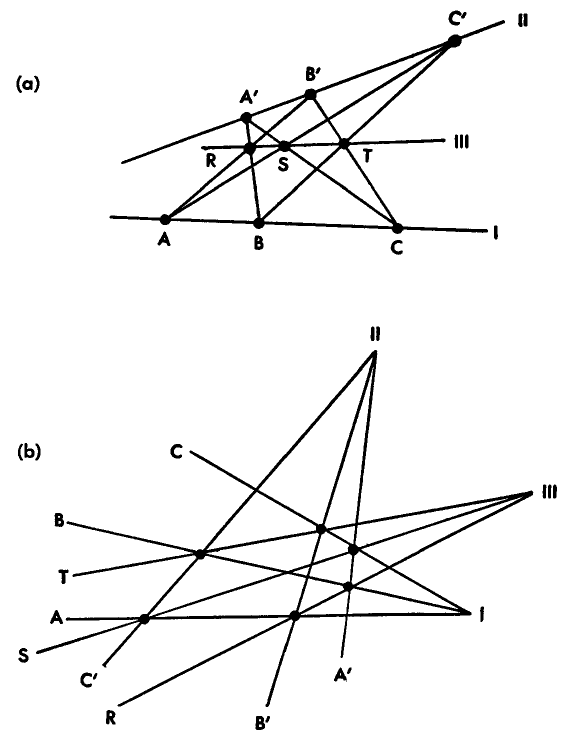
FIGURA 3. La figura 3(a) ilustra el teorema de Pappus: Si A, B, C son tres puntos distintos cualesquiera de una línea I, y A’, B’, C’ tres puntos cualesquiera de otra línea II, los tres puntos R, S, T determinados por los pares de líneas AB’ y A’B, BC’ y B’C, CA’ y C’A, respectivamente, son colineales (esto es, están en la línea III).

La figura 3(b) ilustra el «duplicado» del teorema anterior: Si A, B, C son tres líneas distintas cualesquiera en un punto I, y A’, B’, C’ tres líneas distintas cualesquiera en otro punto II, las tres líneas R, S, T determinadas por los pares de puntos AB’ y A’B, BC’ y B’C, CA’ y C’A, respectivamente, son copuntuales (esto es, tienen el punto III).

Las dos figuras tienen la misma estructura abstracta, aunque sean en apariencia notablemente distintas. La figura 3(a) está referida a la figura 3(b) de tal modo que los puntos de la primera corresponden a líneas de la segunda, mientras que la líneas de la primera corresponden a líneas de la segunda. De hecho, (b) es una proyección de (a): un punto de (b) representa (o es la " imagen reflejo" de) una línea de (a), mientras que una línea de (b) representa un punto de (a).

La característica fundamental de la representación es que puede demostrarse que una estructura abstracta de relaciones existente en un campo de «objetos» existe también entre «objetos» (generalmente de un tipo distinto que los del primer grupo) pertenecientes a otro campo diferente. Esta característica es lo que impulsó a Gödel a construir sus pruebas. Si, como él esperaba, unas complicadas proposiciones metamatemáticas acerca de un sistema formalizado de aritmética pudiesen ser traducidas a (o reflejadas por) proposiciones aritméticas contenidas dentro del propio sistema, se habrá dado un gran paso en el camino de facilitar las demostraciones metamatemáticas. Porque, así como es más fácil manejar las fórmulas algebraicas que representan (o reflejan) intrincadas relaciones geométricas entre curvas y superficies en el espacio que manejar las propias relaciones geométricas, del mismo modo manejar las contrapartidas aritméticas (o «imágenes reflejadas») de complejas relaciones lógicas es más fácil que manejar las relaciones lógicas mismas.

La explotación de la idea de la representación es la clave de la argumentación del famoso trabajo de Gödel. Siguiendo el estilo de la paradoja richardiana, pero evitando cuidadosamente la falacia involucrada en su construcción, Gödel demostró que las proposiciones metamatemáticas acerca de un cálculo aritmético formalizado pueden efectivamente ser representadas por fórmulas aritméticas dentro del cálculo. Como con más detalle explicaremos en el capítulo siguiente, ideó un método de representación tal, que ni la fórmula aritmética correspondiente a una determinada proposición metamatemática verdadera acerca de la fórmula ni la fórmula aritmética correspondiente a la negación de la proposición son demostrables dentro del cálculo. Como quiera que una de estas fórmulas aritméticas debe codificar una verdad aritmética, ninguna de las cuales es, sin embargo, derivable de los axiomas, los axiomas son incompletos. El método de representación de Gödel le permitió también construir una fórmula aritmética correspondiente a la proposición metamatemática «el cálculo es consistente» y demostrar que esta fórmula no es demostrable dentro del cálculo. De ahí se desprende que la proposición metamatemática no puede ser demostrada a no ser que se utilicen reglas de deducción que no puedan ser representadas dentro del cálculo, de tal modo que, al demostrar la proposición, se deben emplear reglas cuya propia consistencia pueda ser tan discutible como la consistencia de la misma aritmética. Gödel demostró y estableció estas importantes conclusiones utilizando una forma sumamente ingeniosa de representación.

VI